Júnior César de Sousa

1 Breve contextualização

Há pouco mais de 5000 mil anos, nas civilizações do Oriente Médio, egípcios e babilônios usavam ferramentas práticas, essenciais a sua vida cotidiana. Podemos dizer, com certa segurança, que foi aí, o berço de toda concepção Matemática; esta era puramente de cunho prático, servindo as necessidades que aqueles povos tinham para prever o melhor tempo da colheita, marcando as estações propícias, e auxiliava o homem na contagem agrária e de seus rebanhos, além de ser fundamental na comercialização de seus produtos. Conta-se, em um relato de Heródoto, que a terra era dividida em lotes de tamanhos iguais, os quais os beneficiários pagavam um aluguel (imposto anual) proporcional e, caso ocorresse uma intempérie natural, a região prejudicada era subtraída proporcionalmente do aluguel de todo terreno.

Os egípcios se destacavam na Geometria, a qual lhes servia para construir enormes pirâmides, bem como se prestava ao cálculo aproximado de volumes e recipientes para carregarem o produto de suas colheitas, aliado a isso, a medição e a marcação de terras (geometrein: geo = terra, metrein = medir) eram fundamentais ao conhecimento dos egípcios, uma vez que, anualmente, as enchentes do rio Nilo destruíam as delimitações, acarretando em novas demarcações, e/ou recálculos proporcionais do imposto, como já mencionado. Além disso, os egípcios se tornaram habilidosos na manipulação das formas e contornos geométricos. Percebe-se por meio do famoso Papiro de Rhind, um texto egípcio pelo qual, os procedimentos realizados eram puramente desprovidos de explicações demonstrativas, apenas se apresentavam como um conjunto de regras a serem aplicadas como verídicas.

Algumas civilizações desapareceram e o poderio, egípcio e babilônico, começou declinar, e em contrapartida, os hebreus, assírios, fenícios e os gregos começaram a ganhar destaque. A invenção alfabética, a criação da moeda e outros fatores propiciaram uma transição do eixo do pensamento. “Quando os gregos deixaram o sul da península balcânica para invadir, estudar e, finalmente, subjugar as antigas civilizações do Oriente Médio, tornaram-se herdeiros de um cabedal matemático acumulado durante séculos.” (BERGAMINI, 1969, p.39). Assumindo todo esse arsenal oriental, os gregos em uma visão mais racionalista e um tanto cética, começaram a se indagar o como e o por quê dos processos os quais os orientais aceitavam como proposições verdadeiras. Com efeito, necessitava-se, então, dar uma feição demonstrativa ao conhecimento poiético dos orientais. Aos poucos, os métodos e os processos matemáticos foram se consolidando, uma vez que o ceticismo grego propiciou o despertar para as realidades abstratas e demonstráveis. Com efeito, tem-se um grande progresso das ciências matemáticas.

A abstração consiste no processo de perceber características/qualidades comuns em coisas diferentes e associá-las a uma regra geral. Enquanto a demonstração é um procedimento que parte de premissas particulares e chega à conclusão geral, aplicável a todos da mesma categoria, destaca-se aqui os postulados, axiomas, as demonstrações por redução ao absurdo, as induções.

Os gregos não se contentavam em mostrar que o resultado dava certo. Queriam explicar o porquê e pelo argumento mais curto e mais estritamente lógico possível. A prova tornou-se uma arte, na qual era ponto de honra a maior economia possível nas etapas do raciocínio, sem deixar qualquer margem a dúvidas. (BERGAMINI, 1969, p.41).

Percebe-se, então, que esses processos citados, são, na verdade, uma sistematização do saber adquirido em terras orientais, formalizando os mesmos, dando-lhes um caráter verídico, não por vias dogmáticas, mas sim, por comprovações passíveis de provas racionais coerentes. Racionalidade essa, que os gregos tanto preconizavam depois que as explicações mítico-fantasiosas já não eram mais suficientes para explicar os fenômenos naturais. É com os gregos, então, que a Matemática torna-se uma ciência mais estruturada.

1.1 A origem do verbete matemática

A palavra matemática se originou do grego μαθηματική (máthema; mathematiké), provavelmente com Pitágoras de Samos (570-496 a.C.), e pode ser traduzida como conhecimento, aprendizagem, tudo aquilo que pode ser aprendido. Como nos relata Nascentes (apud TAHAN, 1961, p. 45) “na Grécia Antiga, [a matemática era compreendida como um] conjunto de conhecimentos, então coordenados, [designava] depois a Astrologia e, finalmente, a ciência dos números, das formas, das relações, das grandezas e dos movimentos.

Atualmente, recebemos a conceituação de Matemática de D’Ambrosio (1990), também seguindo as origens da palavra, diz que, “matema é uma raiz difícil, que vai na direção de explicar, de conhecer, de entender; e tica vem sem dúvida de techne, que é a mesma raiz de arte e de técnica”. Podemos também conceituar a matemática como uma ciência numérica abstrativa que se adapta aos objetos da realidade sensível. Essa realidade sensível é a plena manifestação da essência matemática impregnada em cada ser, isto é, em cada ser subsiste uma realidade instintivamente matemática. Isso significa que embora a matemática seja uma ciência teorética, sendo abstrata e não se preocupe em ter uma utilidade prática, ela pode se adaptar/ajustar aos objetos, tendo conotação também usual e prática, sem que necessariamente seja sua finalidade, mas sim consequência.

1. 2 O desenvolvimento das ciências matemáticas

Pode-se dizer que a revolução do pensamento grego se deve, em parte, a Geometria. A principal fonte de pesquisa no que tange aos primórdios da matemática grega está contida no Sumário Eudemiano, compilado por Proclo (ou Proclus 410- 485 d.e.c.). Nele, consta que Tales viajava pelo Egito, aprendendo aquela ciência (saberes dos antigos “matemáticos” e astrônomos), e pode também descobrir muitas proposições e, posteriormente, pode ensinar a seus discípulos acerca dos conhecimentos adquirido dos egípcios. Este texto, que dista mais de 1000 anos após Tales, caracteriza-o como o primeiro matemático

A partir de Tales de Mileto (625 – 547 a.C.), a Matemática ganha uma nova propulsão, sendo caracterizada como uma ciência mais sistematizada e estruturada. Atribui-se também a Tales, o início da filosofia grega. Como se percebe este pensador desempenhou uma revolução no pensamento; sendo um divisor de águas que impulsionou o avanço da sistematização racional do pensamento. Filosofia e Matemática se encontravam nos primórdios como partes de uma mesma ciência, por isso, não é de se estranhar que a maioria dos primeiros filósofos também contribuíram com suas teorias no campo matemático, interligando tais ciências, embora há quem considere a matemática como predecessora da Filosofia, considerando a primeira, como a mãe de todas as ciências ou a rainha das ciências. Fato é como afirma Giordani (1986) que:

Os helenos herdaram um precioso legado de técnicas fundamentais […] que continham uma ciência implícita a espera dos intelectuais que extraíssem as devidas deduções teóricas e anunciassem o conjunto resultante sob a forma de um sistema lógico e coerente […] Aos helenos coube a missão notável de transformar parte desse acervo em uma verdadeira ciência autônoma […] Na medida em que é explicativa e ontológica, a ciência é uma criação do gênio grego. (GIORDANI, 1986, p.412-413)

Com efeito, podemos dizer que a ciência, como um todo, tem seu berço em território grego, uma vez que é aí o início da sistematização do saber.

2 Tales, o sábio de Mileto

Sabemos que a figura de Tales, bem como a de outros pensadores, é imprecisa historicamente, uma vez que suas obras se perderam ao longo do tempo. Crê-se que a autoria de uma tese era atribuída a seu mestre, dificultando saber a verdadeira autenticidade dos documentos. Com efeito, faz-se necessário confiar na tradição e em documentos posteriores aos quais referencia os pensadores mais antigos.

Tales, como se sabe, era da colônia de Mileto (atual região da Turquia). Dizem que era mercador, tornando-se rico com suas viagens. Atribuem-se a ele várias descobertas matemáticas, entre as quais elucidamos algumas:

a) o cálculo da altura de uma pirâmide egípcia, utilizando sua sombra;

b) qualquer diâmetro efetua a bissecção do círculo em que é traçado;

c) os ângulos da base de um triângulo isósceles são iguais;

d) pares de ângulos de duas retas que se interceptam são congruentes (opostos pelo vértice);

e) se dois triângulos têm dois ângulos iguais e um lado respectivamente igual, são iguais;

f) cálculo da distância de um navio a praia;

g) demonstrações, como, por exemplo, a soma dos ângulos internos de qualquer triângulo é igual a 180º;

h) prova de que todo ângulo inscrito em um semicírculo é um ângulo reto (90º);

i) semelhança de triângulos e proporcionalidade, entre outros.

Tais proposições eram gerais e se aplicavam a qualquer ente geométrico relacionado a cada uma das elucidações. Isso garantia a matemática grega um caráter de totalidade e um método em que é fundamental a comprovação formal. Por sua genialidade, Tales é considerado um dos sete sábios antigos.

3 Pitágoras e os pitagóricos

Sem dúvida, o representante mais notável dos pitagóricos é o seu fundador, Pitágoras de Samos ( 572 a.C.), que provavelmente foi aconselhado por Tales, muitos anos mais tarde, a viajar, assim como ele, para compreender melhor a Matemática. Pitágoras confiava demasiadamente no estudo da Matemática e, em especial, da Filosofia, tendo-a como base moral para a conduta. As próprias palavras Matemática (o que é aprendido) e Filosofia (amor ou amante a sabedoria) foram por ele criadas, descrevendo assim, as atividades intelectuais pessoais e de sua escola que, por sua vez, é permeada de um grande misticismo numérico e religioso. Acreditava na doutrina da metempsicose, segundo a qual, devido a uma culpa primeira, a alma reencarna sucessivas vezes, inclusive sobre diferentes formas, de modo a purificar/expiar da culpa inicial. Os pitagóricos atribuíam à Ciência o melhor caminho de purificação para as almas, e que o fim da vida, compreende justamente, a libertação da alma do corpo.

Dentro da perspectiva matemática pitagórica, destacamos o programa de estudo composto pelas quatro pilares do saber antigo; o quadrivium pitagórico era composto pelas quatro artes que sintetizam bem a concepção matemática da época, a saber: a Aritmética que representava os números em repouso, a Música que era considerada os números em movimento, a Geometria que era as formas em repouso e, por fim, a Astronomia, que seria as formas em movimento. (RAAD, 2009 ^[1]). As exaltações dos números pelos pitagóricos os levaram a atribuição de características místicas aos mesmos e chegou Pitágoras a afirmar que o principio de todas as coisas era o número (entendido não na perspectiva numérica). “Tudo é número”, afirmavam. A oralidade dos ensinamentos era marca da irmandade pitagórica, levando-nos, assim como em Tales, saber a verdadeira autoria das descobertas matemáticas, por isso, prefere-se neste caso, dizer que a contribuição dos pitagóricos, em vez de se referenciar somente a Pitágoras.

Os pitagóricos desempenharam um papel importante, talvez o crucial na história da Matemática. A nova ênfase dada a Matemática, como disciplina de estrutura intelectual e discussão filosófica dos princípios – deferia da conferida pelos egípcios e mesopotâmios – se deve principalmente aos pitagóricos. Para eles a Matemática se relaciona mais com o amor a sabedoria do que com as exigências da vida prática^[2].

Vê-se, portanto, a grande fraternidade matemática e filosófica para a aquisição do saber e posterior desenvolvimento das ciências como forma estruturada do saber e do pensar.

3.1 Os pitagóricos e a música

Motivados pela musicalidade dos golpes de martelos sobre uma bigorna de uma ferraria, os pitagóricos descobriram que as relações com os números inteiros podiam ser interpretados também como intervalos musicais, observando aí, uma harmonia entre os sons produzidos e os números inteiros (em frações simples). Conforme o comprimento de uma corda, ao esticá-la e tencioná-la, produzirá um som diferente, acima ou abaixo do tom inicial. Supõem-se, como podemos verificar em algumas antigas gravuras, que Pitágoras usava sinos, cordas tensionadas, colunas de ar e garrafas d’água para elucidar sua teoria sobre a harmonia musical. “Por exemplo, 16/15 da corda dó é a nota abaixo, si; 6/5 dela é o lá; 4/3 de lá é a corda sol; 3/2 é o fá; 8/5, o mi; 16/9 representa o ré; e exatamente o dobro da corda original, leva-nos outra vez ao dó, uma oitava abaixo.” (BERGAMINI, 1969, p.42-43)

Os pitagóricos acreditavam que os números e suas relações regiam padrões harmônicos e estéticos, por isso, imaginava que o movimento dos planetas era emitido uma harmonia celeste (de números inteiros) ou, como eles diziam, “música das esferas”, ou mesmo como elucidavam ao dizer que a Astronomia era as formas em movimento.

3.2 O teorema de Pitágoras

Sem dúvida, uma das contribuições mais famosas dos pitagóricos é o teorema que leva o nome do fundador da escola, embora, “esse teorema já era conhecido pelos babilônios dos tempos de Hamurabi […] mas sua primeira demonstração geral pode ter sido dada por Pitágoras.” (EVES, 2008, p.103). Isso ressalta que o pensamento oriental era um saber mais prático, como já dito, e que os gregos formalizaram, dando um corpo mais teórico e estruturado, pautado na sistematização do saber.

O teorema de Pitágoras é aplicável aos triângulos retângulos (que possui um ângulo de 90º) e é assim enunciado: o quadrado da hipotenusa é igual a soma dos quadrados dos catetos, algebricamente representado por a² = b² + c². Sua aplicabilidade é muito extensa e recorrente, seja em problemáticas da própria ciência matemática, seja na aplicabilidade prática em determinados setores, como a arquitetura e construção civil (esquadro).

3.3 Os irracionais

A descoberta dos números ditos Irracionais, isto é, aqueles que não podem ser escritos na forma fracionária p/q, com p e q inteiros e, por conseguinte, são dízimas não periódicas (ad infinitum), gerando uma grande crise na escola pitagórica, uma vez que pensavam que a Geometria e a Aritmética poderiam se interligar por intermédio dos números inteiros. Esta descoberta afetou o pensamento matemático grego. Com efeito, a Geometria passou a ser vista apenas sob a ótica apenas das formas e das figuras. Os pitagóricos passavam, então, a marcar geometricamente os pontos correspondentes aos números irracionais, muito presentes nas relações dos triângulos retângulos e nas relações da circunferência.

A propósito, a relação entre o comprimento da circunferência e seu diâmetro é dado por um número irracional que gira em torno de 3,141592654…, denominado de π (lê-se Pi), nome originário da palavra grega periphereia, que significa periferia, no caso da circunferência seria o contorno, isto é, o comprimento da circunferência. Daí se origina o termo perímetro.

4 Razão áurea e os padrões estéticos: a matemática da beleza

Os gregos, como sabemos, prezavam muito pela beleza estética, refletida, sobretudo, em suas esculturas e magníficas construções. As relações de beleza estavam intimamente ligadas a uma proporção, denominada Média e extrema razão (razão áurea, proporção áurea, número de ouro, seção áurea, que, por sua vez, se traduzem no mesmo significado e que estão relacionadas diretamente à sequência de Fibonacci)

A razão áurea […] representa a mais agradável proporção entre duas medidas. Os gregos antigos a designavam como“divisão de um segmento em média e extrema razão” ou simplesmente secção”. No inicio do século XXI convencionou-se identificá-la pela letra grega Φ (Phi maiusculo) (lê-se: Fi), em homenagem ao arquiteto e escultor Phidias, responsável pelo templo grego Parthenon. Φ é o numero irracional 1,618… obtido matematicamente através de sequências continuas infinitas, deduções algébricas ou geométricas. (QUEIROZ, 2007, p.04)

Utilizada em muitas obras famosas, a razão áurea está presente na natureza, no corpo humano, no Universo; também há indícios de seu emprego na construção das pirâmides egípcias, cada bloco era aproximadamente 1,618 vezes maior que o bloco imediatamente superior; há relatos que afirmam que no interior das câmaras das pirâmides, os comprimentos das salas eram 1,618 vezes maiores que as respectivas larguras. Além de estar na estrutura da maioria das plantas, desde o caule até as folhas, garantindo melhor absorção de luz etc., também se pode detectá-la na construção das espirais dos furacões, das galáxias, em vibrações sonoras, até no DNA e em muitas outras ocasiões (no que tange à sequência de Fibonacci^[3]). Nas artes pictóricas e em composições clássicas, notamos que é frequente o uso da razão áurea. No campo literário, há quem afirme que no poema épico de Homero, Ilíada,o qual narra os acontecimentos da famosa Guerra de Tróia, exista uma proporção, entre estrofes maiores e menores, que gira em torno de 1,618, ou seja, o famoso número de ouro, e também noutras obras clássicas.

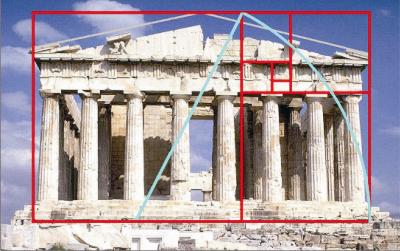
Segundo alguns estudiosos, uma das mais famosas obras arquitetônicas dos gregos, o Pathernon, construído durante o século de Péricles, ainda quando tinha seu frontispício intacto, possuía uma razão entre altura e largura que se aproximava do número Phi. Segundo se relata, o construtor Phidias se preocupava na harmonia da construção. Em muitas literaturas, a respeito do número Phi, desacreditam a possibilidade dessa recorrência no Pathernon, Figura 1, senão por simples intuição.

.

.

.

.

.

.

.

.

O retângulo áureo, Figura 2, é uma das formas geométricas mais apreciadas pela beleza artística, e se manifestando em muitas construções, desde os monumentais gregos até a arquitetura moderna.

.

.

.

.

.

.

.

Na Figura 3, é dada a sua construção geométrica, a partir de um quadrado ABFE, sendo o retângulo áureo dado por EFCD.

.

.

.

.

.

.

No reino animal e vegetal é grande a recorrência do número de ouro (e da sequência de Fibonacci), mas é importante salientar que os autores nem sempre convergem ao explicitar as recorrências da razão áurea nas áreas já mencionadas, Antônio Gonzales Neto (apud GIMENEZ, 2011) nos diz sabiamente que: “O mais irracional dos números regula a estética e a natureza.”

4 Euclides de Alexandria

Atribui-se ao matemático helenístico Euclides (cerca de 300 a.e.c.) à coordenação e sistematização de todo trabalho matemático-geométrico de seus antecessores, compilando todo arsenal clássico em uma obra denominada Os Elementos, dividida em treze capítulos. “Nenhum trabalho, exceto a Bíblia, foi tão largamente usado ou estudado e, provavelmente, nenhum exerceu influência maior no pensamento científico” (EVES, 2008, p.167). A importância dessa obra é inestimável e foi, por muitos anos, a principal fonte de estudo de Geometria.

5 Considerações finais

Segundo Durant,

Além da contribuição para a formação de um vocabulário técnico a Grécia Antiga está presente na ciência moderna […] com os princípios fundamentais formulados por seus matemáticos [gregos]. [Estes] fundaram os alicerces da Trigonometria e do cálculo, propiciaram e terminaram o estudo das secções cônicas e elevaram a geometria tridimensional a tanta perfeição, que até ao advento de Descartes e Pascal essa ciência permaneceu como eles a haviam deixado. (apud GIORDANI, 1986, p. 492)

A importância da Matemática e sua consolidação foi um longo processo, reconhecido e confirmado pela posteridade; Platão chegou a afirmar, em seu livro a República, que esta ciência (aritmética) era indispensável à formação dos governantes ideais e até mesmo fundamental ao desenvolvimento estratégico nas guerras. Segundo Platão, as ciências matemáticas não é uma simples ciência, é acima um estudo humanístico, sem o qual “o Homem não seria Homem”, despertando neste, o despertar do pensamento. Nesse contexto, pode-se dizer que as matemáticas são como que propaidéias, isto é, antecessoras basilares que preparam a Paidéia. (JAEGER, 1995, p. 897-898)

Vale ainda ressaltar que a notação matemática grega antiga era bem precária (simbologia cuneiforme) o que torna o despertar grego às ciências matemáticas ainda mais valoroso. A notação científica que atualmente usamos começa a ser mais difundida com René Descartes, no século XVII. Enfim, podemos, ao término desse trabalho, ressaltar a grande importância que as Ciências Matemáticas desempenharam ao longo de toda a formação do pensamento grego antigo, propiciando todo um arsenal intelectivo, pautada no conhecimento racional dos fatos, na análise crítica e sistematizada do saber, onde a mera praticidade se torna consequência, uma vez que como ciência teorética, a Matemática busca o saber pelo próprio saber.

De fato, vale ressaltar a grande importância do legado oriental que propiciou aos gregos darem um enfoque mais abstrativo e geral a essa ciência, a ponto de ser considerada, por muitos, como a mãe de todas as ciências ou mesmo a rainha das ciências, exaltando assim, o grande benefício para o desenvolvimento das demais ciências e para o desenrolar, não somente do pensamento grego, mas de toda uma compreensão acerca das ciências. Por fim, vale ressaltar que a Matemática não era concebida de maneira isolada, uma vez que por ciência se compreendia uma gama de conhecimentos que eram agregados e usados em comum, mas para fins diversos. Mas, certamente, a ramificação da Matemática destaca-se dentre os demais conhecimentos adjacentes, por motivos já elucidados, e por si mesma, tem seu valor em si e por si. Podemos considerar, então, a Matemática inútil e totalmente útil, dependendo do uso a ser feito dela, embora sua finalidade se basta em si mesma.

Referências

BERGAMINI, David et al. O pensamento geométrico dos gregos antigos. In: ______. As matemáticas. Rio de Janeiro: Livraria José Olympio Editora, 1969.

D’AMBROSIO, Ubiratan. Etnomatemática. São Paulo: Ática, 1990

EVES, Howard. Introdução à história da Matemática. Trad. Hygino H. Domingues. Campinas: Unicamp, 2008.

GIORDANI, Mário Curtis. As ciências. In: ______. História da Grécia: antiguidade clássica I. 4. ed. Petrópolis: Vozes, 1986, p.411-421

GIMENEZ, Karine. Proporção ou Razão Áurea: o princípio da arquitetura estrutural e da arte. Disponível em: <http://ddesigndeinteriores.blogspot.com.br/2011/02/proporcao-ou-razao-aurea-o-principio-da.html> Acesso em 30 jun. 2012.

JAEGER, Werner. As matemáticas como propaidéia. In: ______. Paidéia:A formação do Homem Grego. Trad. Artur M. Parreira. 3. ed. São Paulo: Martins Fontes, 1997, p.896-909.

QUEIROZ, Rosania Maria. Razão Áurea: a beleza de uma razão surpreendente. Universidade Estadual de Londrina, Londrina, 2007. (Programa de Desenvolvimento Educacional)

TAHAN. Malba. Origem da palavra Matemática. In: ______. Didática da matemática. 3. ed. São Paulo: Saraiva, 1961, p. 45-56

.